A magia do juro composto
Um espetáculo de magia de teor financeiro.
Em 2014, a história de Ronald Read tomou de assalto todas as manchetes dos principais meios de comunicação social americanos ligados à esfera financeira. A razão? A sua capacidade em ter conseguido amealhar uma fortuna de mais de 8 milhões de dólares até à sua morte, já com 92 anos. Deverá estar-se a interrogar o que é que há de tão espetacular e especial em relação a mais um executivo de uma empresa cotada na bolsa americana, que recebeu bónus chorudos e salários de sete dígitos durante toda a sua carreira, e que deixou uns milhões para a próxima geração. A questão é que esta persona que acabei de descrever, e que provavelmente idealizou no seu pensamento não é Ronald Read. Estamos a falar de alguém que auferiu salários modestos (para a realidade americana) enquanto jardinheiro e funcionário numa bomba de gasóleo durante toda a sua vida. Assim de repente, parece que estamos perante uma autêntico encanto de magia digno de entrada no quadro de honra de Hogwarts. No entanto, a história de Ronald Read não é fictícia, é bem real. Não teve um único pingo de magia. A realidade é que costuma pregar-nos partidas e ocasionalmente tem um tempero mágico.
“Compound interest is the eighth wonder of the world. He who understands it, earns it; he who doesn’t, pays it.”
Albert Einstein
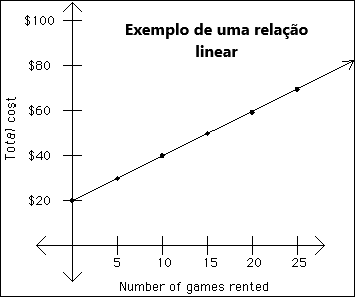
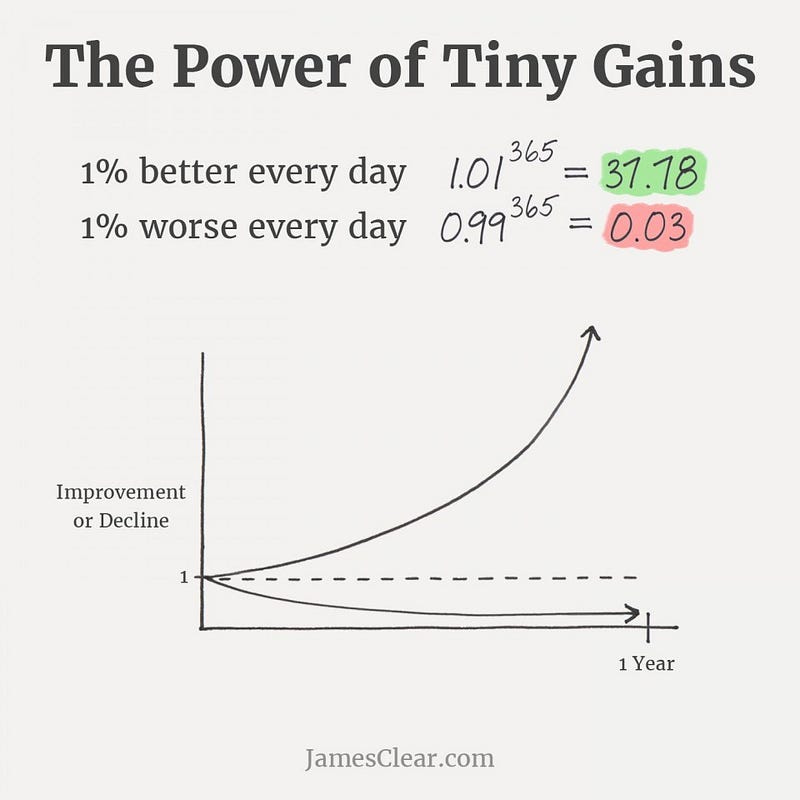
A nossa realidade está sobrecarregada de relações lineares. O nosso salário baseia-se na venda do nosso tempo por um determinado preço por hora. Se trabalharmos 8 horas num dia, o nosso salário diário será o preço que acordámos vezes 8. Se nos deslocarmos a uma velocidade média de 50km/h, a distância percorrida será igual à duração da viagem vezes a velocidade a que nos deslocámos. Se a viagem tiver o dobro da duração, ceteribus paribus, teremos percorrido o dobro da distância. Estando completamente submersos num ambiente recheado de linearidade, é perfeitamente natural que o nosso cérebro tenha dificuldade em processar uma realidade paralela onde o mundo funciona de forma diferente. Até na própria aritmética encontramos exemplos. Uma operação de soma como 8+8+8+8+8 acaba por ser muito mais intuitiva do que uma operação de multiplicação como 8*8*8*8*8. Relações não lineares não encaixam no cérebro humano.
Existem vários géneros de relações não lineares que fazem parte da nossa realidade, no entanto foquemo-nos agora no tipo que nos poderá catapultar para outros horizontes e outras fronteiras: relações exponenciais, mais concretamente a aplicabilidade do famoso juro composto no crescimento do nosso dinheiro.
Uma ideia completamente incorreta que ainda perdura na cabeça de muitos de nós, é a de que o juro ou retorno que possamos obter sobre as nossas poupanças e investimentos, apresenta uma relação linear, através do chamado juro simples. Assumindo um depósito a 5 anos de 5000 euros a 2% e uma relação linear constante, um juro anual constante de 100 euros durante a duração do depósito seria a nossa remuneração neste cenário hipotético, como podemos observar na tabela.
Porém, este raciocínio é completamente falacioso. O potencial crescimento do nosso capital apresenta uma relação exponencial, não linear. No primeiro ano, o juro será semelhante. Mas no segundo ano, o juro incidirá não só sobre o capital inicial, como também no juro obtido no primeiro ano. No terceiro ano, o juro incidirá não só não só sobre o capital inicial, como também no juro obtido no segundo ano, para além do juro do primeiro ano.
Ano 0 – 5000
Ano 1 – 5000 + 2% de 5000 = 5100
Ano 2 – 5000 + 100 + 2% de 5000 + 2% de 100 = 5202
Ano 3 – 5000 + 100 + 110 + 2% de 5000 + 2% de 100 + 2% de 110 = 5306.4
O que se sucede é uma espécie de juro sobre o juro que vai crescendo de forma exponencial ao longo do tempo. Uma bola de neve que vai ganhando cada vez mais tração à medida que o tempo vai passando. É através desta tendência exponencial que explicamos a força do juro do composto.
A trajetória de crescimento de um investimento de 10 mil dólares com 15% de retorno anual ao longo de 40 anos leva-nos até mais de 2 milhões e meio de dólares. Falamos de multiplicar o nosso capital mais de 250 vezes!
Existem várias histórias que ilustram de forma bastante vívida o poder dominador da oitava maravilha do mundo. Conta a lenda que há milhares de anos atrás, um rei indiano lançou um concurso aos seus cidadãos para criar um jogo que combatesse o seu aborrecimento. Um dos concorrentes criou o jogo de xadrez, perfazendo assim as necessidades de entretenimento do imperador. Dado a sua satisfação e contentamento com o jogo, este questionou que recompensa o camponês desejaria como fruto do seu trabalho. Encontrará a sua icónica resposta no parágrafo em baixo.
“Oh emperor, my wishes are simple. I only wish for this. Give me one grain of rice for the first square of the chessboard, two grains for the next square, four for the next, eight for the next and so on for all 64 squares, with each square having double the number of grains as the square before.”
Inicialmente o imperador ficou espantado pelo facto do inventor ter requerido uma recompensa tão pequena. Passado uma semana, percebeu que não iria ter capacidade de pagar a sua dívida, pois no 64º e último quadrado iria ter de entregar 18,000,000,000,000,000,000 grãos de arroz, sensivelmente 210 mil millhões de toneladas, o que seria suficiente para cobrir a superfície da Terra.
“The most powerful force in the universe is coumpound interest.”
Albert Einstein
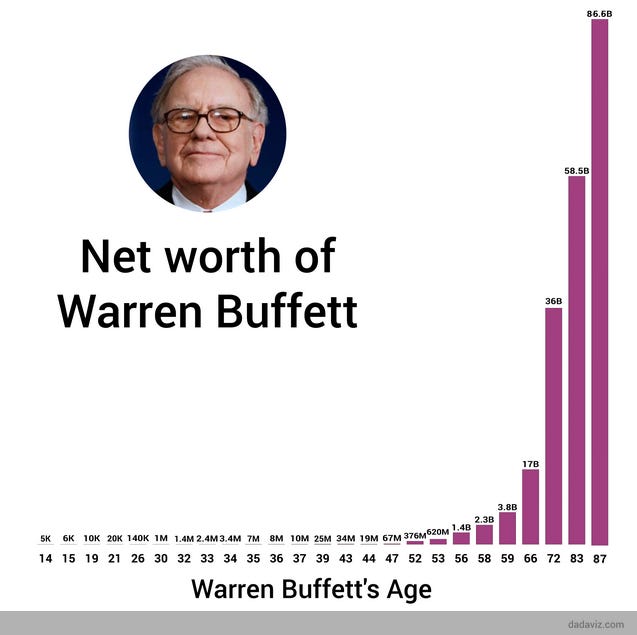
Em The Price of Tomorrow, Jeff Booth refere mais um exemplo do potencial sobrenatural do juro composto, através do poder deflacionário exponencial da tecnologia. Se um ser humano tivesse capacidade para dobrar uma folha A4 50 vezes, a espessura da folha chegaria até ao Sol! Mas o melhor exemplo será o crescimento da fortuna daquele que é considerado por muitos, o melhor investidor de todos os tempos, Warren Buffett. Os nossos cérebros não estão preparados para lidar com estas abominações.
“My wealth has come from a combination of living in America, some lucky genes, and compound interest.”
Warren Buffett
Quantificar o impacto da inflação na desvalorização do nosso dinheiro é outro excelente exemplo de como confundimos relações lineares com relações exponenciais. Caso o preços de um cabaz de bens e serviços custe 100 euros hoje, inflação de 5% durante 5 anos, significa que esse mesmo cabaz custará 127.62 euros e não 125 euros como alguns poderão idealizar.
Como podemos então maximizar todo o poder e a força do juro composto em prol da nossa saúde financeira?
A fórmula matemática do juro composto é baseada em 3 variáveis: capital investido, retorno sobre o capital e duração do investimento. Não necessitamos de um doutoramento em ciências matemáticas para concluir que quanto maiores forem estes 3 inputs, maior será a força exponencial que irá empurrar as nossas finanças pessoais para um pedestal de tranquilidade relativamente a preocupações financeiras. Analisemos agora em mais detalhe o que poderemos relativamente a cada uma das três variáveis.
Montante Investido — P
Quanto mais capital conseguirmos poupar, mais “material” o juro composto terá para trabalhar. Para termos mais poupança, teremos de ganhar mais ou gastar menos (ou ambos). Num país marcado por rendimentos baixos, a ginástica necessária para esticar os nossos níveis de poupança será sempre complexa. Negociar salário, trocar de trabalho frequentemente, colocar o dinheiro de parte antes de gastá-lo e lançar um side hustle são exemplos de pequenas práticas que poderão ajudar a acumular um pouco mais de poupança ao final do mês.
Retorno/Juro — i
Como John Boogle e Burton Malkiel demonstram em The Little Book of Common Sense Investing e A Random Walk Down Wall Street respetivamente, tentar obter de forma consistente um retorno superior ao mercado é um jogo de perdedores. E não podemos descurar todo o tempo e esforço empregue nesse processo nem o custo emocional de lidar com maior volatilidade no portefólio e de tomar decisões sobre a nossa carteira. Um fundo indexado de baixo custo acaba por ser sempre uma melhor opção. (Warren Buffett aprova esta sugestão) Atenção também aos custos de gestão associados aos vários produtos financeiros como fundos de investimento e PPRs. Pagar 1.5% ao ano de comissões de gestão, pode parecer pouco à primeira vista, mas se tivermos em atenção o seu efeito na limitação do poder exponencial do juro composto, rapidamente percebemos que esse efeito é tudo menos reduzido.
Impacto de diferentes custos de gestão para um portefólio de 1 milhão de dólares com 6% de retorno anual para um horizonte temporal de 30 anos. A diferença entre 1% e 2.5% é de mais de um milhão e 500 mil dólares no final dos 30 anos.
Investimentos em outras classes de ativos (negócio próprio, imobiliário) também poderão ser boas alternativas, dependendo sempre do conhecimento específico de cada investidor.
Duração do Investimento — n
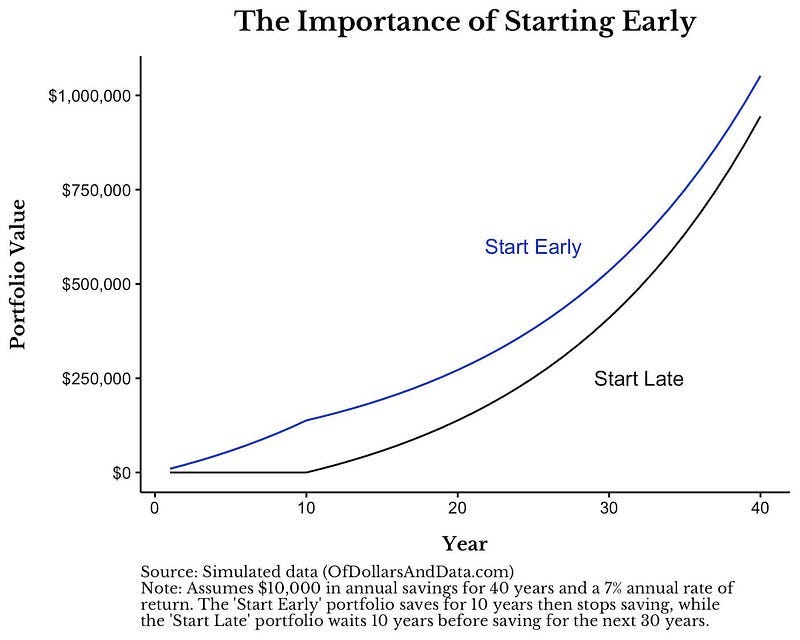
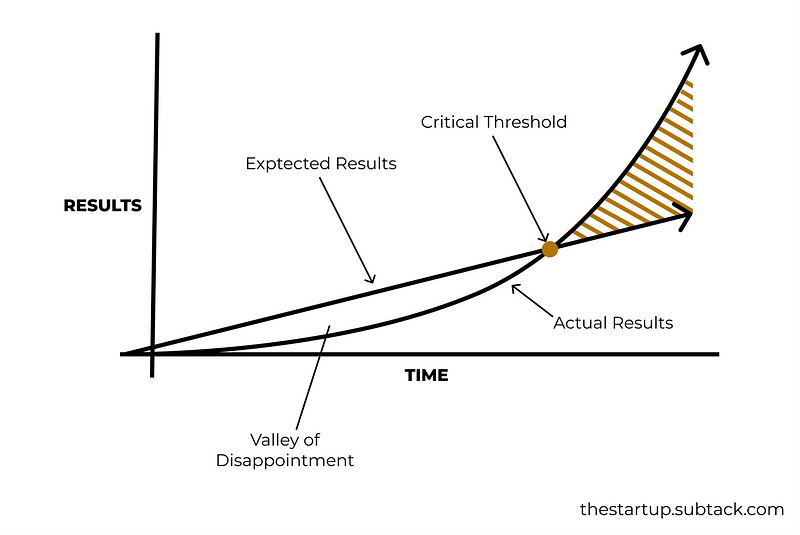
Esta variável é a que tem mais influência no bolo final. E a mais fácil de maximizar o seu impacto. O melhor dia para começar a investir era ontem. O segundo melhor dia é hoje. Quanto maior for a duração do nosso investimento, maior será a probabilidade de assistirmos a crescimentos exponenciais do nosso património semelhantes aos de Buffett. (com a devida proporção claro) Como já tivemos oportunidade de observar no gráfico anterior, os retornos absolutos gordos e saborosos irão acontecer décadas depois de iniciarmos a nossa jornada enquanto investidores. Quanto mais cedo sairmos da partida, mais rapidamente chegaremos à meta. Sempre que deixar passar mais um dia, o preço a pagar será cada vez maior, visto que está a limitar a capacidade exponencial de alavancar o seu património. Afinal de contas, o nosso ativo mais precioso não é o nosso dinheiro, mas sim o nosso tempo. Um aforrador que invista durante 10 anos e pare de investir nos 30 anos seguintes, terá mais capital acumulado ao final de 40 anos do que alguém que tenha esperado 10 anos, e tenha investido nos 30 anos seguintes exatamente os mesmos montantes.
“Someone is sitting in the shade today because someone planted a tree a long time ago.” — Warren Buffett
É tão importante o juro composto ser nosso escravo e trabalhar para nós, como é fundamental não sermos nós os escravos a trabalhar para ele, evitando ao máximo que a oitava maravilha do mundo se transforme num par de algemas. Refiro-me naturalmente à epidemia económica que assola praticamente todos os agentes económicos nos dias de hoje: dívida.
Se as nossas despesas forem superiores aos nossos rendimentos, temos um problema sério em mãos. Ao contrário dos governos, não temos nenhum banco central a que possamos recorrer que tenha a capacidade de imprimir dinheiro para alimentar a nossa compaixão por gastar dinheiro.
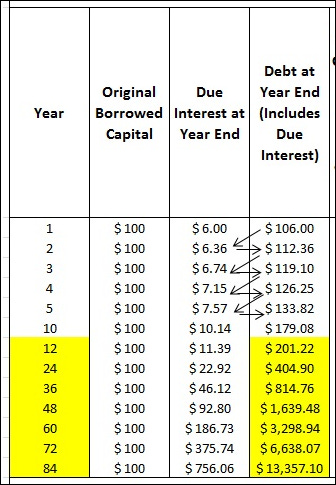
Suponhamos que pedimos 100 euros emprestados a um juro de 6% anual para nos ajudar a financiar a compra de um novo modelo do iPhone. Caso não liquidemos o empréstimo logo de seguida, esses 100 euros vão crescendo de forma exponencial ao ponto de que passado 10 anos, o valor em dívida chega ao dobro do montante que pedimos inicialmente emprestado. Imaginemos agora que em vez de 100 euros, falamos de 10000 euros com juros anuais de 16%. Digam adeus à nossa liberdade. Digam olá a uma sociedade de escravos.
É curioso que as implicações do juro composto vão muito para além das questões financeiras. Se refletirmos nas nossas rotinas, encontramos relações exponenciais com bem maior frequência do que o que imaginaríamos. O meu exemplo preferido é o conceito que James Clear introduz no seu best seller Atomic Habits de como pequenas mudanças acabam por fazer toda a diferença num horizonte de tempo mais alargado.
“Understanding both the power of compound interest and the difficulty of getting it is the heart and soul of understanding a lot of things.”
Charlie Munger
Até aqui conseguimos observar a dificuldade que nós humanos temos em compreender relações exponenciais. Quando iniciamos algo novo, temos a expectativa de que os nossos resultados serão proporcionais linearmente ao nosso trabalho e ao nosso esforço. Desde as nossas relações pessoais até à criação de novos negócios, o compouding das nossas ações só terá o devido efeito mais tarde. Ninguém conhece alguém que tenha tido resultados 1 mês depois de se inscrever no ginásio. Mas há quem acredite que 4 semanas de treino são suficientes para estar em forma como o LeBron James. A realidade simplesmente não funciona dessa forma.
“Most people overestimate what they can do in one year and underestimate what they can do in ten years.”
Bill Gates
Agora que já injetámos uma boa dose de exponencialidade no seu cérebro, a receita para tirar partido do juro composto é simples: comece a investir o mais cedo possível, afaste-se ao máximo possível de qualquer crédito não produtivo, construa bons hábitos e deixe a magia acontecer!
Boas poupanças e bons investimentos!
Ainda não subscreveu o blog? Está na hora de subscrever o The Money Game!